机器学习笔记【人工神经网络-上】
前言
本节本来很多都是证明过程,看了看似懂非懂(是我没好好学数分了)于是也都没有记下来。随便记了点东西。
神经元的MP模型
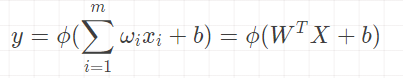
找到合适的向量W和b
感知器算法(二分类问题)
目标函数
若 ,则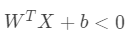
若 ,则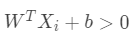
算法步骤
随机选择 W和b
取训练样本(X,y)
若
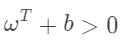
且 则: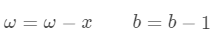
若
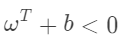
且 则: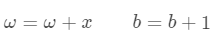
再取一个训练样本,重复 2 直至收敛
终止条件:直到所有输入输出对 (X,y),都不满足2中两条件,则退出循环
多层神经网络
由线性的神经元和层与层之间的非线性变换组成,若非线性函数是阶跃函数,则三层的神经网络可以模拟任意的决策函数
算法结构(神经网络层数与每层神经元个数)与问题难度匹配
算法模型复杂度与训练样本复杂度匹配
梯度下降法求局部极值
证明好大一堆,不敲了。基本上就是利用泰勒展开求局部极值。对于多层,用链式求导来简化计算(后向传播算法 从后往前求偏导)。
后向传播法基本框架
对神经网络每一层的各个神经元,随机选取相应的 w,b的值
向前计算,对于输入的训练数据,计算并保留每一层的输出值直到最后一层的输出y
设置目标函数E,如
 用后向传播算法对每一个W和b,计算:
用后向传播算法对每一个W和b,计算: .
.利用梯度下降法,更新W与b
回到2,直到所有
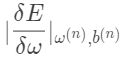
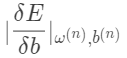
很小为止
算法改进
非线性函数选择
由于阶跃函数在x=0无导数,影响偏导数的求解。
常用替代
SIGMOID函数 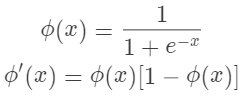
thanh函数(双曲正切)
目标函数设置
独热向量解决多分类问题
SOFTMAX函数加交叉熵作为目标函数
随机梯度下降法 SGD
不是每输入一个样本就更新参数,而是输入一批样本(BATCH | MINI-BATCH)球的这些样本的梯度平均值后,根据这个平均值改变参数。在神经网络的训练中BATCH的样本数(BATCH SIZE)大致设为50-200
每训练所有数据一次为一个EPOCH,每个EPOCH要随机打乱训练样本次序以增加BATCH的随机性
上期问题
在上一次,说到关于拟合度的问题。个人的理解是,SVM作为一个全局求唯一解的算法,核函数的设置会导致过拟合或欠拟合。最后估算的正确率并不准确。很明显,由于上期的代码最后用的是总数据计算的超平面,又拿总数据来做验证,是不合理的。较准确的准确率应为相应超参数在交叉验证下的正确率 约为99.9%。