机器学习干货篇:人工神经网络(上)
从本次开始我们将要深入机器学习领域当中很重要的分支——人工神经网络(Artifical Neural Network,ANN),它是现今最火热的人工智能研究的方向——深度学习的基础。而此次我们从人工神经元模拟生物神经元开始切入,再到人工神经元组合构成人工神经网络模型,进而简单介绍人工神经网络的核心算法。
01 神经元
人工神经元,简称神经元,是构成神经网络的基本单元。受生物学的启发,人工神经网络是生物神经网络的一种模拟。它从结构、实现机理和功能上模拟生物神经网络,传统的生物神经元模型由树突、细胞核、细胞体、突触和神经末梢组成,如下图所示。
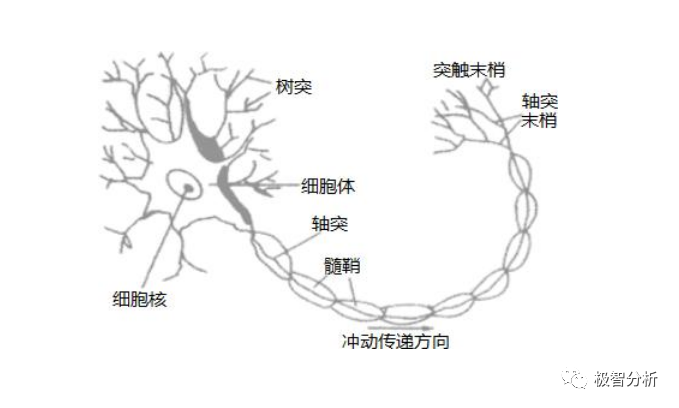
那么人工神经元是如何模仿生物神经元呢?神经元的输入xi对于生物神经元的树突。输入xi向细胞体传播脉冲,相当于输入权值wi,通过细胞核对输入的数据和权值参数进行加权求和。传播细胞体的脉冲相当于人工神经元的激活函数,最终输出结果的y作为下一个神经元的输入。
上述为人工神经网络中最基本的处理单元——神经元,主要由连接、求和节点、激活函数组成。
连接:神经元中数据流动的表达方式。
求和节点:对输入信号和权值的乘积进行求和。
激活函数:一个非线性函数,对输出信号进行控制。
为了方便理解,我们对生物神经元抽象,得到神经元的基本模型,如下图所示
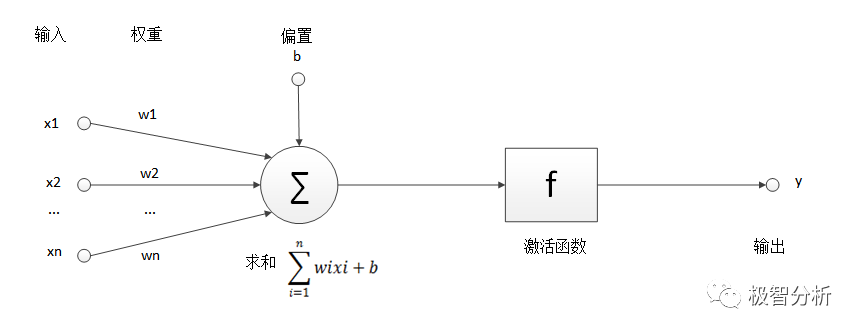
其中:x1,x2,...,xn为输入信号的各个分量; w1,w2,...,wn为神经元各个突触的权值;b为神经元的偏置参数;∑为求和节点,z=x1w1+x2w2+...+xnwn+b,f为激活函数,一般为非线性的函数,如Sigmoid,Tanh函数等;y为神经元的输出。
02 激活函数性质
在正式了解神经网络激活函数之前,我们首先思考几个问题,为什么需要激活函数,如何选择激活函数?
首先看看激活函数在神经网络模型中的位置,如上图中激活函数实际上隐藏在神经网络模型中的连接线上,该连接线包括输入矩阵与权值相乘的过程,还包括激活函数对数据激活的过程。
激活函数的一般性质如下。
1.单调可微
一般情况下,我们使用梯度下降的算法更新神经网络中的参数,因此必须要求激活函数可微。如果激活函数是单调递增的,求导后函数必大于零(方便计算),因此需要激活函数具有单调性。
2.限制输入范围
输入的数据通过神经元上的激活函数来控制输出值的大小,该输出的数值是一个非线性的。一般我们根据阈值来判断是否需要激活该神经元。
3.非线性
因为线性模型的表达能力不够,因此激活函数的出现还为神经网络模型中加入了非线性的因素。
03 激活函数介绍
激活函数拥有上述特性,它存在的意义在于:一个没有激活函数的神经网络只不过是一个线性回归模型,它不能表达复杂的数据分布。神经网络中加入激活函数,相当于引入了线性因素,从而解决了线性模型不能解决的问题。
接下来开始简单介绍几个激活函数。
1. Sigmoid 函数
Sigmoid型函数是指一类S型曲线函数如下图所示,对于S(x),若x→无穷,则S’(x)→0(S’(x)表示s(x)的导数)。
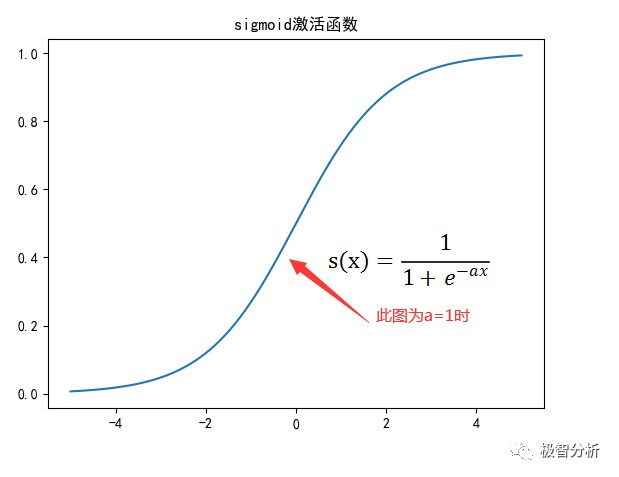
优点:
1.Sigmoid函数的输出范围在[0,1]之内,函数单调连续,优化稳定;
2.函数求导方便;
3.输出可以看做概率分布,使得神经网络可以更好地和统计学习模型进行结合,可以用在输出层。
缺点:
1.Sigmoid函数容易饱和,导致训练结果不佳;
2.其输出不是零均值,数据存在偏差,分布不平均。
2.Tanh 函数
如下图所示,双曲正切函数(Tanh)与Sigmoid函数类似,不同的是Tanh的值范围为-1到1,因此Tanh的优点是可以更容易地处理负数。同时,Tanh是0均值,也就解决了Sigmoid函数的非0均值的缺点,所以实际中Tanh函数会比Sigmoid函数更常用。
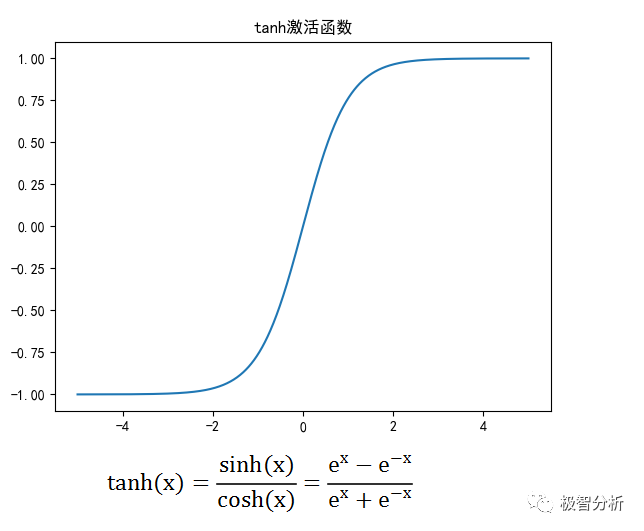
优点:
1.Tanh函数比Sigmoid函数收敛速度更快,更加易于训练;
2.输出值是以0为中心,数据分布均匀。
缺点:
1.没有改变Sigmoid函数由饱和性引起的梯度消失问题。
3.ReLU函数
研究表明大脑同一时刻大概只有1%~4%的神经元处于活跃状态,表明神经元工作的稀疏性。从信号方面来看,神经元同时只对输入信号的少部分进行选择性响应,大量的信号被刻意屏蔽,可以提高神经网络的学习精度,更好地提取稀疏特征。
而ReLU也叫Rectifier函数(如下图所示)则满足仿生学中的稀疏性,只有当输入值高于一定数目时才激活该神经元节点。当输入值低于0时进行限制,当输入上升到某一阈值以上时,函数中的自变量与因变量呈现线性关系。
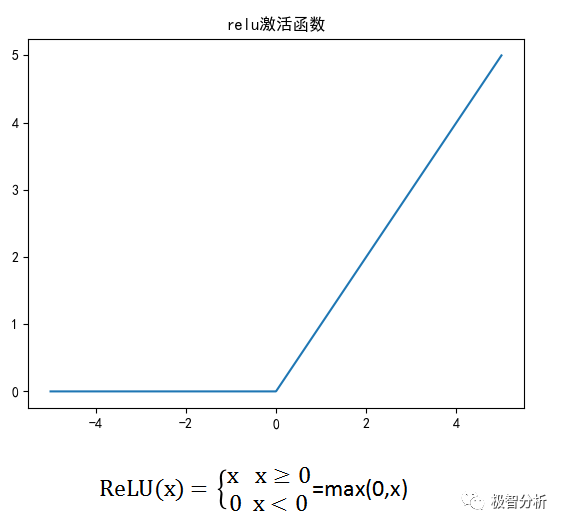
优点:
1.相比Sigmoid函数和Tanh函数,ReLU函数在随机梯度下降算法中能够快速收敛;
2.ReLU函数的梯度为0或常数,因此可以缓解梯度消失问题;
3.ReLU函数引入稀疏激活性,在无监督训练时也能有较好的表现。
缺点:
1.ReLU神经元在训练中不可逆地死亡;
2.随着训练的进行,可能会出现神经元死亡、权重无法更新的现象,流经神经元的梯度从该点开始将永远是零。
4. Softmax函数
Softmax函数的本质是将一个K维的任意实数向量,映射成另一个K维的实数向量,其中向量中的每个元素取值都介于(0,1)之间。
Softmax是对逻辑回归(Logistic Regresion)的推广,逻辑回归用于处理二分类问题,而Softmax回归则用于处理多分类问题。
如下图所示,在数学上Softmax函数会返回输出类的互斥概率分布,通常把Softmax作为输出层的激活函数。
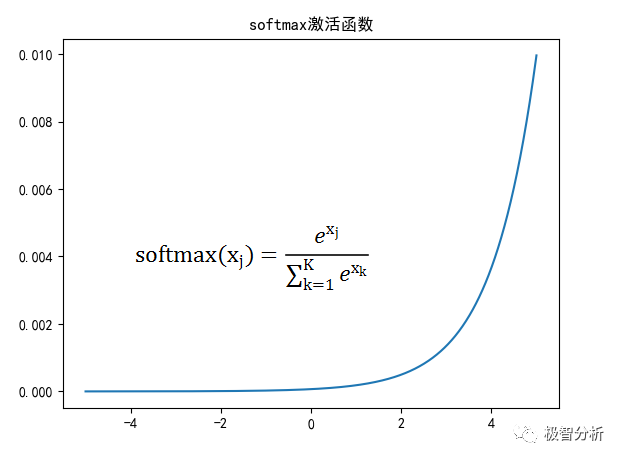
04 激活函数的选择
选择激活函数时,一般隐藏层选择ReLU函数会得到较为理想的效果。当然这不是恒定的规律。我们可以尝试使用Sigmoid函数作为隐藏层激活函数,但注意使用时尽量不要超过太多的隐藏层。
另外可以使用Tanh函数来代替Sigmoid函数观察模型的ROC曲线。如果直接使用ReLU函数作为激活函数,注意梯度下降算法的学习率参数不要设置过高,避免神经元的大量“消亡”。
对于输出层,一般使用Softmax函数获取同分布最高概率作为输出结果。
对于神经网络的其他知识,下期将为您讲解。请持续关注我们!
参考文献:
【1】陈仲铭、彭凌西 深度学习原理与实践[M]. 人民邮电出版社,2018.
【2】邱锡鹏 神经网络与深度学习[M]. 机械工业出版社,2020.
结语
临床研究的根本使命是发现并解决生命科学领域亟待解决的临床问题,同时,为即将发生的临床难题提供备选解决方案。
打开极智分析—智能医学统计分析平台 https://www.xsmartanalysis.com/ 进行实操吧!
点击“阅读全文”参加有奖问卷活动,内含超大福利,不要错过哦!
往期精彩回顾
【2】原来喝咖啡竟可以防心衰,快来看看这篇文章是怎么研究的吧

扫二维码
关注我们
公众号|极智分析
B站|极智分析
THE END

