机器学习-分类（人工神经网络）

逻辑斯蒂回归本质上可以视为一个计算单元。即输入n个x,对输入进行加权（n个w）,再加上偏置之后进行求和；求得的和作为1个输入input,然后对输入进行sigmoid非线性转换，最后输出。人工神经网络其实是对计算单元的扩充。

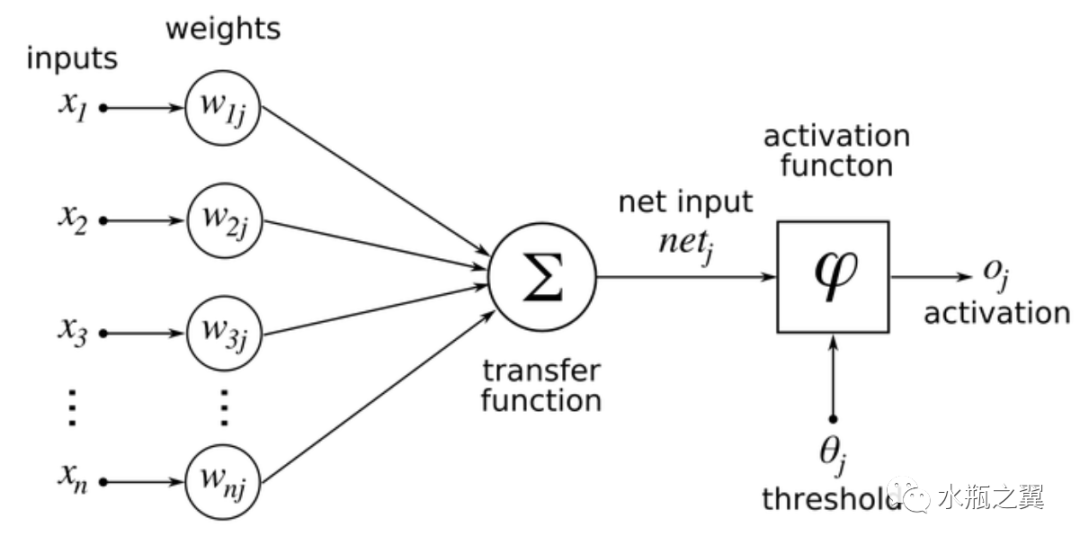
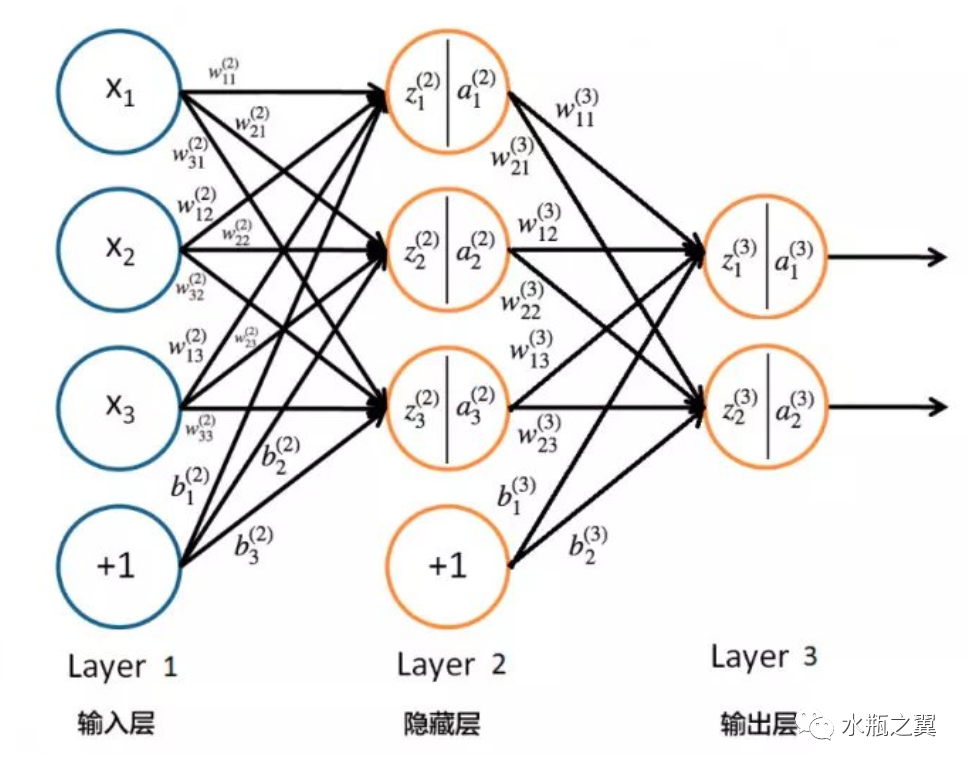
人工神经网络的学习（BP神经网络）

确定层级，节点数以后，任务就是学习/拟合到不同的 w 权值
类似于逻辑斯蒂回归，可以通过梯度下降的方法。先随机生成若干个神经元上的w，再寻找到误差平方和最小的 w 。
寻找梯度的重要原理：误差反向传播（链式法则），w不断迭代更新。
算法语言
输入：
D由训练元组和目标值组成的数据集；
λ学习率；
network多层前馈神经网络（网络结构：多少层，每层几个节点）
输出：
训练后的神经网络（将相应的w进行优选了）
R语言实现
nnet 包部分参数：size 单隐藏层节点数。Wts 权重系数，绝大多数情况下不设定，即随机生成。rang 随机生成的区间[-rang , rang]，一般是0.5。decay 控制所训练的网络的泛化能力，默认为0。maxit 最大迭代次数，默认为100。MaxNWts 最大的 w 数量，一般不需要设置。

留出法人工神经网络模型训练

1. 载入数据，留出法得到训练集和测试集

rm(list = ls())
load('data/cjb.rda')
library(tidyverse)
cjb <- cjb %>% select(3:13) %>% mutate(wlfk = factor(wlfk))
set.seed(2012)
train_set_idx <- sample(nrow(cjb), 0.7 * nrow(cjb))
test_set_idx <- (1:nrow(cjb))[-train_set_idx]

2. 用nnet包进行人工神经网络训练

library(nnet)   # nnet包，单隐藏层
set.seed(2012)
imodel <- nnet(wlfk ~ .,
               data = cjb[train_set_idx, ],
               size = 7)  # size没有默认值，不可少
names(imodel)  # 看一下imodel这个列表有哪些组成部分

##  [1] "n"             "nunits"        "nconn"         "conn"         
##  [5] "nsunits"       "decay"         "entropy"       "softmax"      
##  [9] "censored"      "value"         "wts"           "convergence"  
## [13] "fitted.values" "residuals"     "lev"           "call"         
## [17] "terms"         "coefnames"     "contrasts"     "xlevels"

imodel$n  # 每一层节点个数，输入层10，隐藏层7，输出层1

## [1] 10  7  1

imodel$wts %>% head # 连接的权值

## [1] -0.3943680  0.3416725 -0.3056565  0.6092443  0.3449834  0.5246967

imodel$fitted.values %>% head # 每一个训练集相应的得到的拟合结果

##          [,1]
## 635 0.1089146
## 28  0.7728674
## 251 0.7728674
## 399 0.1089146
## 329 0.7728674
## 159 0.7728674

# 训练集拟合效果
predicted_train <- predict(imodel,newdata = cjb[train_set_idx,],
                           type = "class")
Metrics::ce(cjb$wlfk[train_set_idx], predicted_train)

## [1] 0.1829945

# 测试集拟合效果
predicted_test <- predict(imodel,newdata = cjb[-train_set_idx,],
                          type = "class")
Metrics::ce(cjb$wlfk[-train_set_idx], predicted_test)

## [1] 0.2403433

3. 神经网络参数的选择

#采用的是caret包中的方法，通过caret包中的grid搜索来进行参数选择
library(caret)
set.seed(2012)
# expand.grid函数，生成一个格子数据框
nn_grid <- expand.grid(size = c(1, 3, 7),
                       decay = c(0.01, 0.03, 0.1))
imodel <- train(wlfk ~ .,data = cjb,method = "nnet",
              maxit = 2000,tuneGrid = nn_grid)

imodel$bestTune # 优选结果

##   size decay
## 6    3   0.1

plot(imodel)  # 绘图查看训练结果

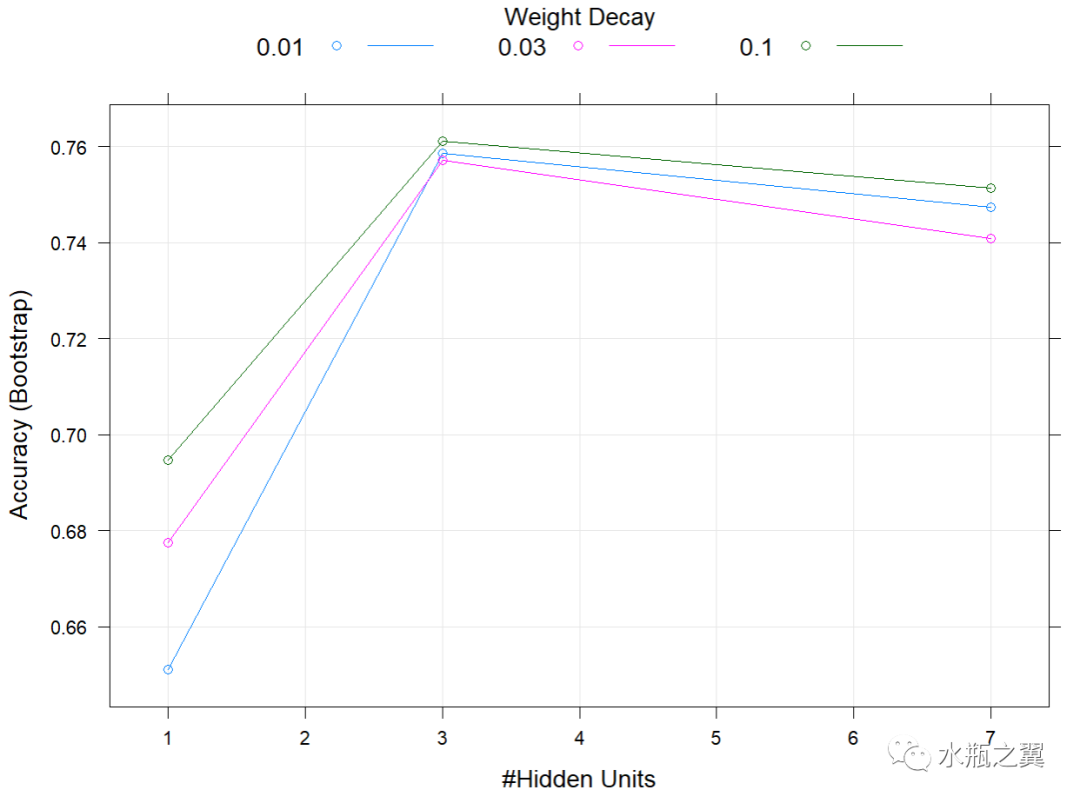
# 参数选择后训练集拟合效果
predicted_train <- predict(imodel,  newdata = cjb[train_set_idx,],
                           type = "raw")
Metrics::ce(cjb$wlfk[train_set_idx],predicted_train)

## [1] 0.2273567

# 参数选择后测试集拟合效果
predicted_test <- predict(imodel,newdata = cjb[-train_set_idx,],
                          type = "raw")
Metrics::ce(cjb$wlfk[-train_set_idx],predicted_test)

## [1] 0.1459227 错误率大大降低

4. 用NeuralNetTools包绘制神经网络

library(NeuralNetTools)
# 使用最佳参数训练模型
imodel2 <-  nnet(wlfk ~ .,data = cjb[train_set_idx,], 
  decay = imodel$bestTune$decay,
  size = imodel$bestTune$size,maxit = 2000)
# plotnet绘制神经网络
plotnet(imodel2,rel_rsc = c(1.8, 3),circle_cex = 3,
  cex_val = 0.75,bord_col = "lightblue",max_sp = TRUE)

I为input，O为output，H为隐藏层，线条粗细代表权值大小

k折交叉检验人工神经网络训练

1. 还是定义那三个函数

# 1. k折交叉检验产生训练集与测试集
cv_kfold <- function(data, k = 10, seed = 2012) {
  n_row <- nrow(data)#计算数据的行数
  n_foldmarkers <- rep(1:k, ceiling(n_row / k))[1:n_row]
  set.seed(seed)
  n_foldmarkers <- sample(n_foldmarkers)  #打乱顺序
  kfold <- lapply(1:k, function(i){(1:n_row)[n_foldmarkers == i]})
  return(kfold)
}
# 2. 模型评估函数imetrics
global_performance <- NULL
imetrics <- function(method, type, predicted, actual) {
  con_table <- table(predicted, actual)
  cur_one <- data.frame(
    method = method,
    #算法模型的名称
    type = type,
    #取值为train或是test
    accuracy = sum(diag(con_table)) / sum(con_table),
    error_rate = 1 - sum(diag(con_table)) / sum(con_table)
  )
  assign("global_performance",
         rbind(get("global_performance", envir = .GlobalEnv) ,
               cur_one),
         envir = .GlobalEnv)
}
# 3. 基于k折交叉检验的模型构建、评估函数
kfold_cross_validation <-
  function(formula, data, kfolds, learner, ...) {
    sp <- Sys.time() #记录开始时间
    cat("\n[Start at:", as.character(sp))
    lapply(kfolds, function(curr_fold) {
      train_set <- data[-curr_fold,] #训练集
      test_set <- data[curr_fold,] #测试集
      predictions <- do.call(learner, args = c(
        list(
          formula = formula,
          train = train_set,
          test = test_set
        ),
        list(...)
      ))
      imetrics(learner,
               "Train",
               predictions$predicted_train,
               train_set$wlfk)
      imetrics(learner,
               "Test",
               predictions$predicted_test,
               test_set$wlfk)
    })
    ep <- Sys.time()
    cat("\tFinised at:", as.character(ep), "]\n")
    cat("[Time Ellapsed:\t",
        difftime(ep, sp, units = "secs"),
        " seconds]\n")
  }

2. 进行k-折交叉检验人工神经网络模型训练

kfolds<- cv_kfold(cjb)
learn.nnet <- function(formula, train, test, ...) {
  imodel_kfold <-  nnet(formula, train, ...)
  predicted_train <-  predict(imodel_kfold, train, type = "class")
  predicted_test <- predict(imodel_kfold, test, type = "class")
  return(list(predicted_train = predicted_train,
              predicted_test = predicted_test))}

kfold_cross_validation(
  formula = wlfk ~ .,
  data = cjb,
  kfolds = kfolds,
  learner = "learn.nnet",
  decay = imodel$bestTune$decay,
  size = imodel$bestTune$size,
  maxit = 2000)
global_performance %>% head

##       method  type  accuracy error_rate
## 1 learn.nnet Train 0.8089080  0.1910920
## 2 learn.nnet  Test 0.7820513  0.2179487
## 3 learn.nnet Train 0.8045977  0.1954023
## 4 learn.nnet  Test 0.8461538  0.1538462
## 5 learn.nnet Train 0.8175287  0.1824713
## 6 learn.nnet  Test 0.7179487  0.2820513