【机器学习】人工神经网络-多层感知器(MLP)对鸢尾花数据集进行分类

一、MLP 原理

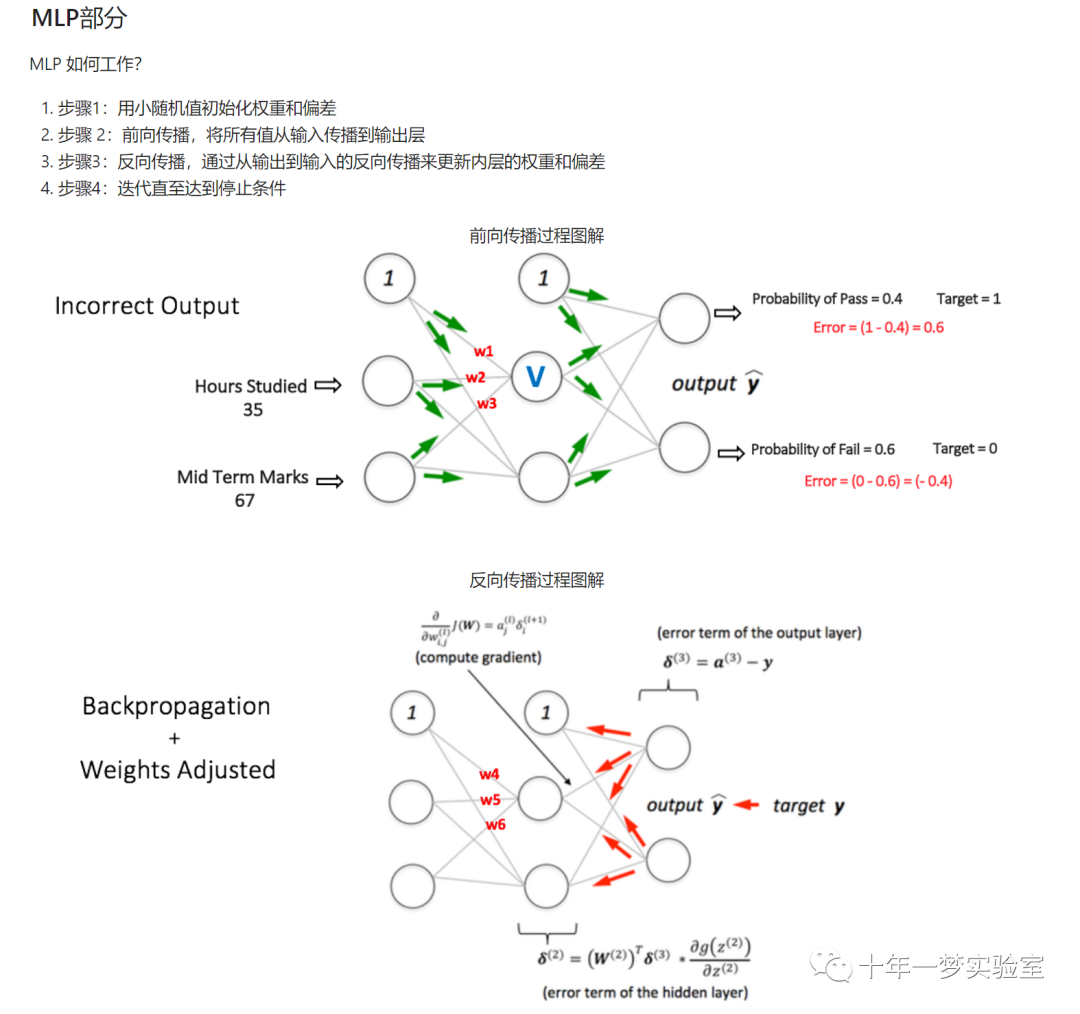
多层前馈型神经网络正向传播算法的流程

Sigmoid函数及其导数

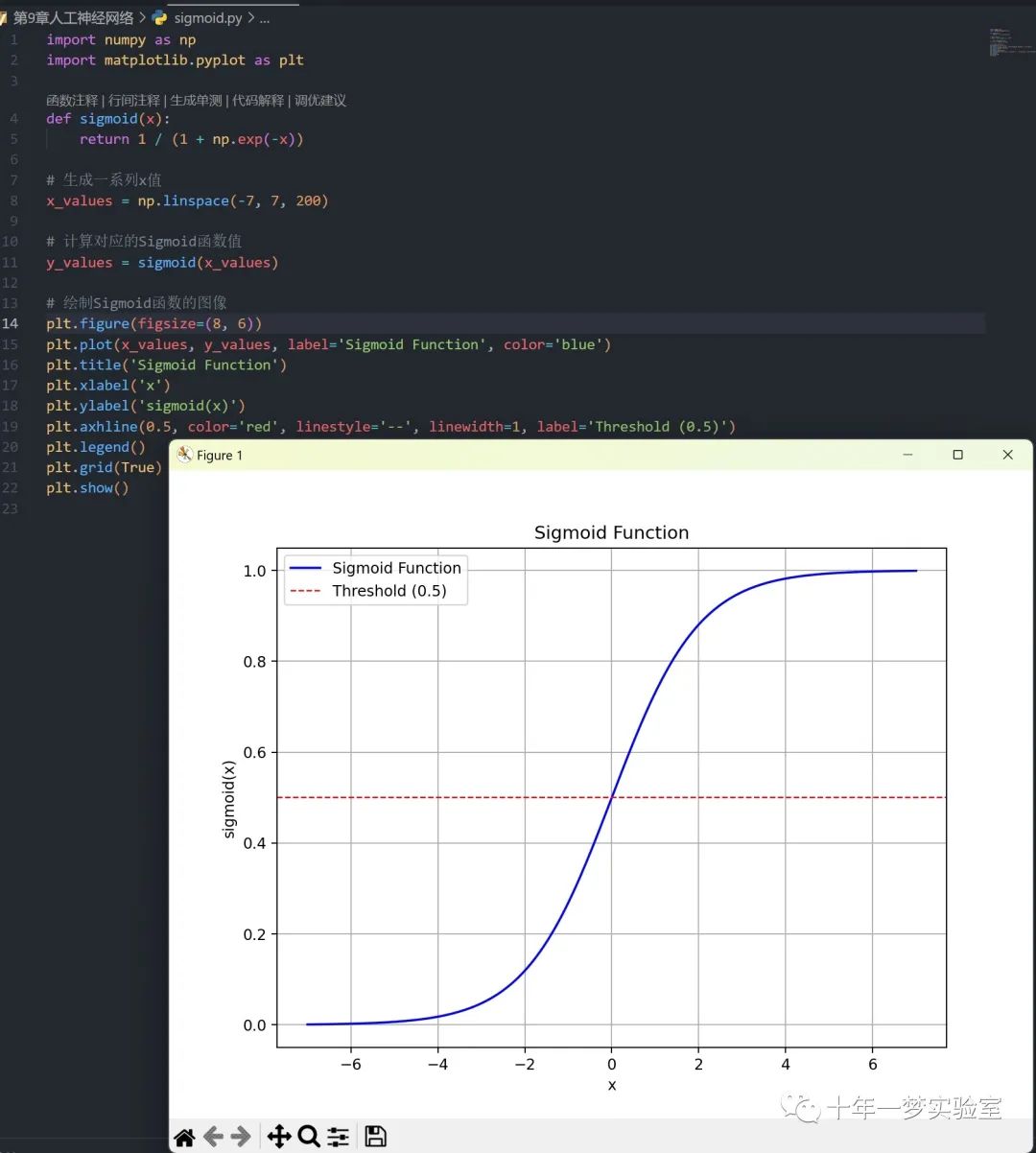

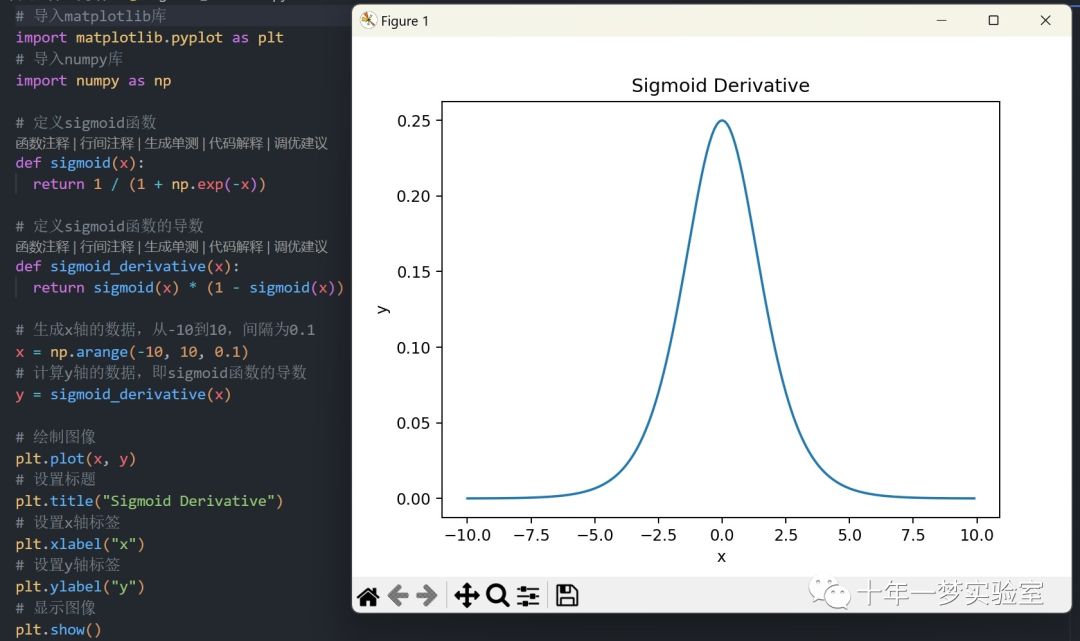
反向传播算法

二、示例-多层感知器(MLP)对鸢尾花数据集进行分类
1. 导入所需的库:导入了用于数据处理、可视化和神经网络的库。
2. 加载和检查数据集:使用 pandas 加载鸢尾花数据集,并进行简要的数据检查。
3. 数据清理过程:将数据集标签进行数字编码,将鸢尾花的三个类别分别编码为数字 0、1 和 2。
4. 将数据集分为训练集和测试集:将数据集分为训练集和测试集,并对数据进行随机排序。
5. MLP 部分:定义了一个 `MultiLayerPerceptron` 类,包含了 MLP 的初始化、权重初始化、激活函数和导数的定义等。
6. 定义反向传播过程算法:在 `Backpropagation_Algorithm` 函数中定义了 MLP 的反向传播算法,用于更新权重。
7. 定义用于绘制每个 epoch 误差值的函数:`show_err_graphic` 函数用于绘制每个 epoch 的误差值图。
8. 定义用于预测测试数据的 `predict` 函数。
9. 定义用于训练过程的 `fit` 函数:`fit` 函数用于训练 MLP 模型。
10. 使用训练数据训练 MLP 模型:使用给定的参数初始化 `MultiLayerPerceptron` 类,然后调用 `fit` 函数进行模型训练。
11. 使用 MLP 模型预测测试数据:使用训练好的 MLP 模型调用 `predict` 函数进行测试数据的预测。
12. 计算混淆矩阵和分类报告:计算混淆矩阵和打印每个类别的精确度、召回率和 F1 分数。
这个代码实现了一个简单的 MLP 模型,并在鸢尾花数据集上进行了训练和测试。请注意,这只是一个基础的实现,实际应用中可能需要进行更多的调优和改进。
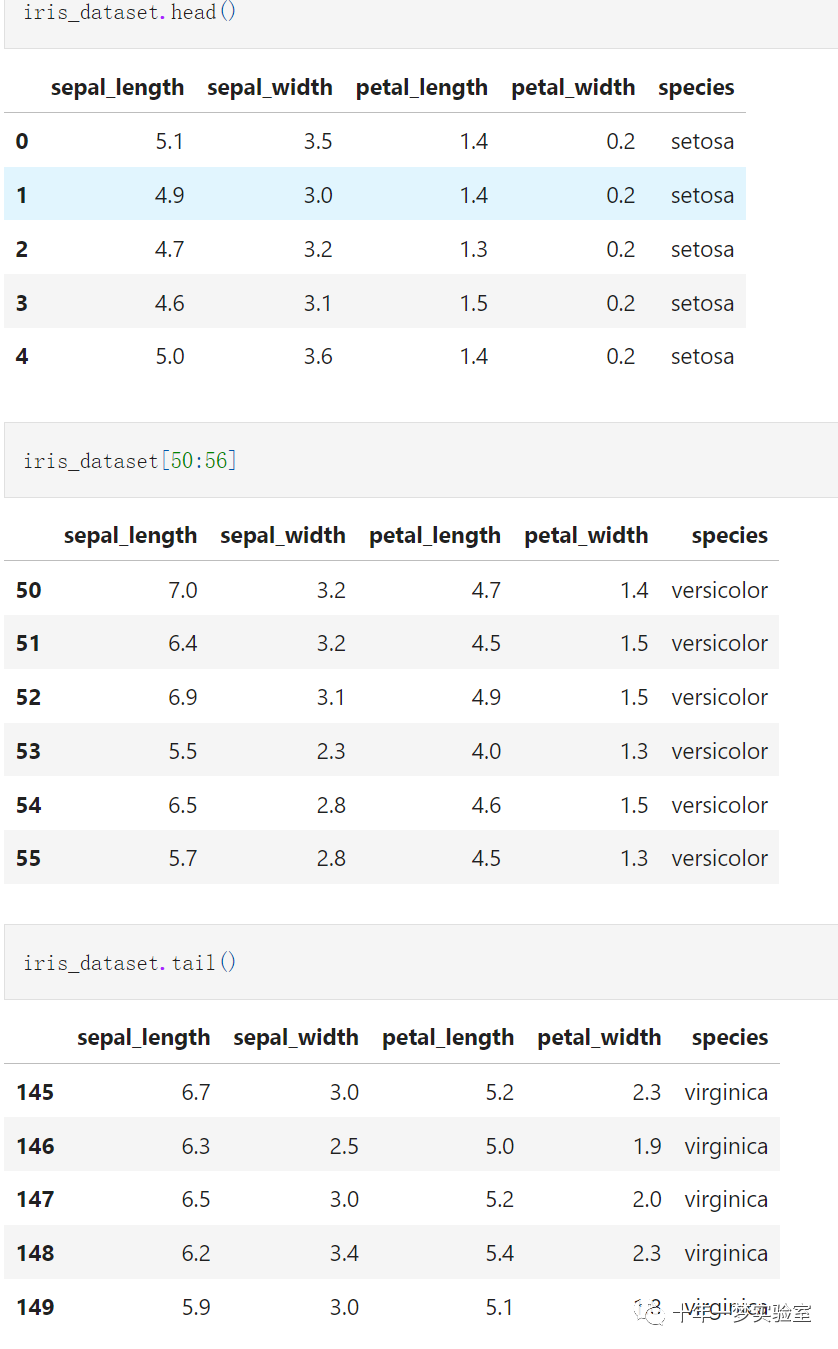
数据集简要信息

# 导入所需的库import os # 用于文件操作from matplotlib import pyplot as plt # 用于数据可视化import pandas as pd # 用于加载和处理原始数据集import numpy as np # 用于数值计算import random # 用于生成随机数from pandas.plotting import scatter_matrix # 用于绘制散点图矩阵
加载和检查数据集
# 加载和检查数据集# 设置工作目录并加载数据os.chdir('./mlp-from-scratch-master/iris_dataset')# 使用pandas读取和检查数据集iris_dataset = pd.read_csv('iris.csv')iris_dataset.head() # 查看数据集的前几行iris_dataset[50:56] # 查看数据集的中间几行iris_dataset.tail() # 查看数据集的后几行
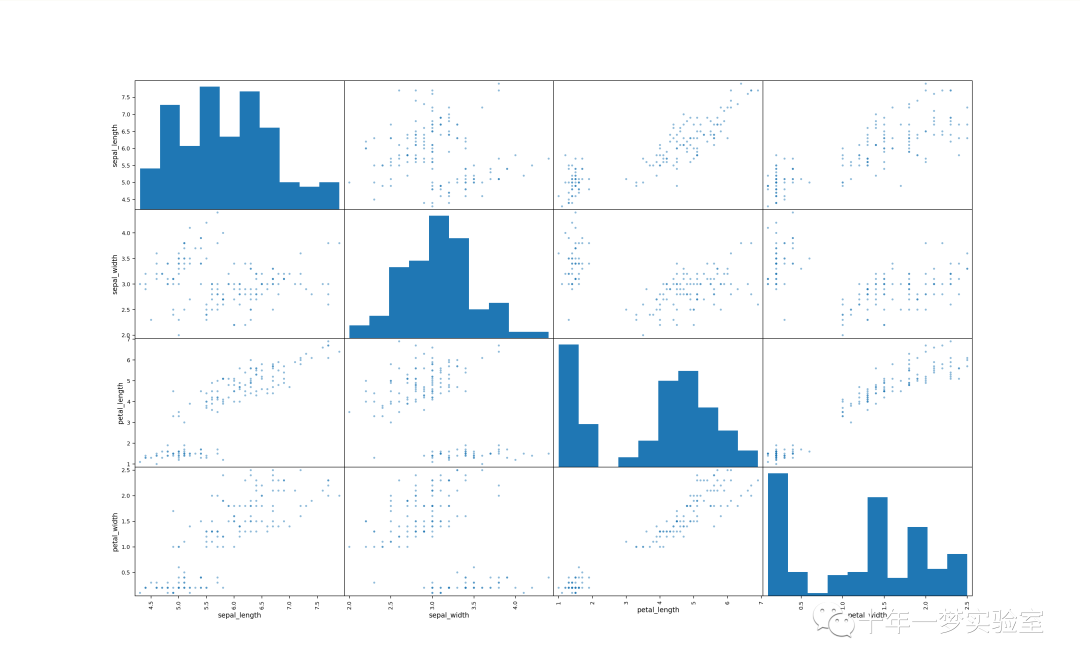
可视化原始数据集
# 可视化原始数据集scatter_matrix(iris_dataset, alpha=0.5, figsize=(20, 20)) # 绘制数据集的散点图矩阵#plt.show() # 显示图像
iris_dataset.plot(subplots=True, figsize=(10, 10), sharex=False, sharey=False) # 绘制数据集的折线图#plt.show() # 显示图像
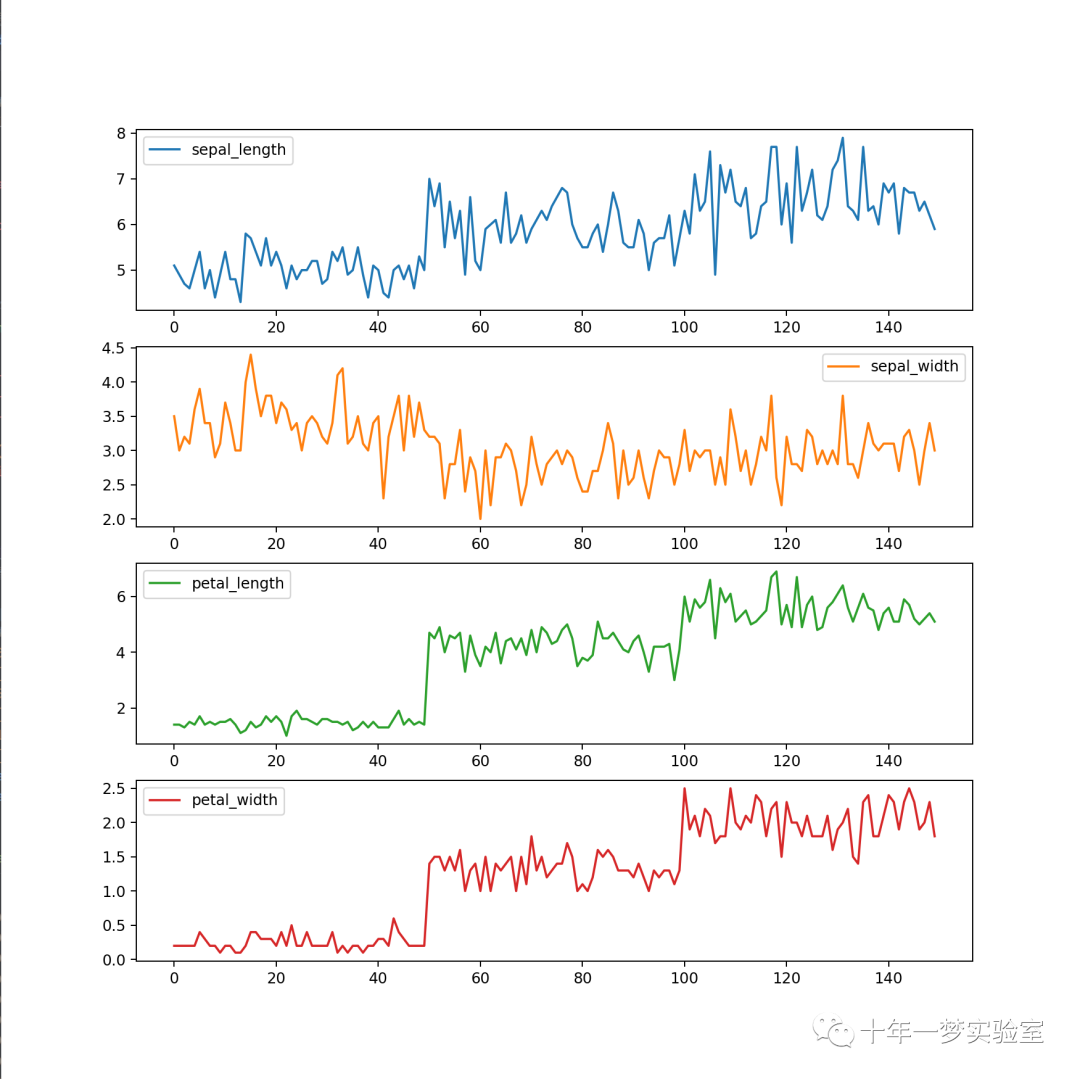
数据清洗流程
# 对数据集的标签进行数字编码,0: Iris-Setosa, 1: Iris-Versicolor, 2: Iris-Virginicaprint('[INFO] create numeric classes for species (0,1,2) ...')iris_dataset.loc[iris_dataset['species']=='setosa','species']=0 # 将setosa替换为0iris_dataset.loc[iris_dataset['species']=='versicolor','species']=1 # 将versicolor替换为1iris_dataset.loc[iris_dataset['species']=='virginica','species'] = 2 # 将virginica替换为2iris_label = np.array(iris_dataset['species']) # 将标签转换为numpy数组iris_data = np.array(iris_dataset[['sepal_length','sepal_width','petal_length', 'petal_width']]) # 将特征转换为numpy数组
划分数据集为训练集和测试集
# 划分数据集为训练集和测试集random.seed(123) # 设置随机数种子def separate_data(): # 定义一个函数,用于划分数据集A = iris_dataset[0:40] # 取每个类别的前40个样本作为训练集tA = iris_dataset[40:50] # 取每个类别的后10个样本作为测试集B = iris_dataset[50:90]tB = iris_dataset[90:100]C = iris_dataset[100:140]tC = iris_dataset[140:150]train = np.concatenate((A,B,C)) # 将不同类别的训练集拼接起来test = np.concatenate((tA,tB,tC)) # 将不同类别的测试集拼接起来return train,test # 返回训练集和测试集print('[INFO] separate data to train data and test data')iris_dataset = np.column_stack((iris_data,iris_label.T)) # 将特征和标签拼接起来iris_dataset = list(iris_dataset) # 将数据集转换为列表random.shuffle(iris_dataset) # 打乱数据集的顺序Filetrain, Filetest = separate_data() # 调用划分数据集的函数#[i[:4] for i in Filetrain]:这是一个列表推导式,它遍历Filetrain列表中的每个元素i,# 对于每个元素i,它取i的前四个值(即i[:4]),并将这四个值作为一个子列表添加到新的列表中。# 这样,新的列表就包含了Filetrain中每个样本的四个特征,而不包括标签。train_X = np.array([i[:4] for i in Filetrain]).astype('float') # 提取训练集的特征,并转换为浮点数train_y = np.array([i[4] for i in Filetrain]).astype('float') # 提取训练集的标签,并转换为浮点数test_X = np.array([i[:4] for i in Filetest]).astype('float') # 提取测试集的特征,并转换为浮点数test_y = np.array([i[4] for i in Filetest]).astype('float') # 提取测试集的标签,并转换为浮点数
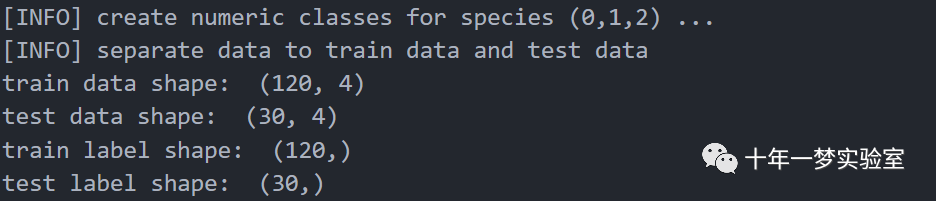
print('train data shape: ', train_X.shape) # 打印训练集的形状print('test data shape: ', test_X.shape) # 打印测试集的形状print('train label shape: ', train_y.shape) # 打印训练集的标签的形状print('test label shape: ', test_y.shape) # 打印测试集的标签的形状
定义多层感知器(MLP)类对象
# 定义多层感知器(MLP)类对象class MultiLayerPerceptron:def __init__(self, params=None): # 定义初始化方法,接受一个参数params# 如果params为空,则使用默认的MLP层参数if (params == None):self.inputLayer = 4 # 输入层的节点数self.hiddenLayer = 5 # 隐藏层的节点数self.outputLayer = 3 # 输出层的节点数self.learningRate = 0.005 # 学习率self.max_epochs = 600 # 最大迭代次数self.BiasHiddenValue = -1 # 隐藏层的偏置值self.BiasOutputValue = -1 # 输出层的偏置值self.activation = self.activation['sigmoid'] # 激活函数self.deriv = self.deriv['sigmoid'] # 激活函数的导数else:# 如果params不为空,则使用params指定的MLP层参数self.inputLayer = params['InputLayer']self.hiddenLayer = params['HiddenLayer']self.OutputLayer = params['OutputLayer']self.learningRate = params['LearningRate']self.max_epochs = params['Epochs']self.BiasHiddenValue = params['BiasHiddenValue']self.BiasOutputValue = params['BiasOutputValue']self.activation = self.activation[params['ActivationFunction']]self.deriv = self.deriv[params['ActivationFunction']]# 初始化权重和偏置值self.WEIGHT_hidden = self.starting_weights(self.hiddenLayer, self.inputLayer) # 隐藏层的权重矩阵self.WEIGHT_output = self.starting_weights(self.OutputLayer, self.hiddenLayer) # 输出层的权重矩阵self.BIAS_hidden = np.array([self.BiasHiddenValue for i in range(self.hiddenLayer)]) # 隐藏层的偏置向量self.BIAS_output = np.array([self.BiasOutputValue for i in range(self.OutputLayer)]) # 输出层的偏置向量self.classes_number = 3 # 类别数passdef starting_weights(self, x, y): # 定义一个函数,用于生成初始的权重矩阵return [[2 * random.random() - 1 for i in range(x)] for j in range(y)] # 生成一个x行y列的随机数矩阵,范围在-1到1之间# 定义激活函数和导数函数,根据数学公式实现activation = {'sigmoid': (lambda x: 1/(1 + np.exp(-x * 1.0))), # sigmoid函数'tanh': (lambda x: np.tanh(x)), # 双曲正切函数'Relu': (lambda x: x*(x > 0)), # 线性整流函数}deriv = {'sigmoid': (lambda x: x*(1-x)), # sigmoid函数的导数'tanh': (lambda x: 1-x**2), # 双曲正切函数的导数'Relu': (lambda x: 1 * (x>0)) # 线性整流函数的导数}# 定义反向传播算法的过程def Backpropagation_Algorithm(self, x): # 定义一个函数,接受一个参数x,表示输入层的数据DELTA_output = [] # 定义一个空列表,用于存储输出层的误差梯度# 第一阶段 - 计算输出层的误差ERROR_output = self.output - self.OUTPUT_L2 # 输出层的误差等于期望输出减去实际输出DELTA_output = ((-1)*(ERROR_output) * self.deriv(self.OUTPUT_L2)) # 输出层的误差梯度等于误差乘以输出层的导数arrayStore = [] # 定义一个空列表,用于存储中间结果# 第二阶段 - 更新输出层和隐藏层的权重和偏置for i in range(self.hiddenLayer): # 遍历隐藏层的每个节点for j in range(self.OutputLayer): # 遍历输出层的每个节点self.WEIGHT_output[i][j] -= (self.learningRate * (DELTA_output[j] * self.OUTPUT_L1[i])) # 更新输出层的权重,使用梯度下降法self.BIAS_output[j] -= (self.learningRate * DELTA_output[j]) # 更新输出层的偏置,使用梯度下降法# 第三阶段 - 计算隐藏层的误差delta_hidden = np.matmul(self.WEIGHT_output, DELTA_output)* self.deriv(self.OUTPUT_L1) # 隐藏层的误差梯度等于输出层的权重矩阵乘以输出层的误差梯度,再乘以隐藏层的导数# 第四阶段 - 更新隐藏层和输入层的权重和偏置for i in range(self.OutputLayer): # 遍历输入层的每个节点for j in range(self.hiddenLayer): # 遍历隐藏层的每个节点self.WEIGHT_hidden[i][j] -= (self.learningRate * (delta_hidden[j] * x[i])) # 更新隐藏层的权重,使用梯度下降法self.BIAS_hidden[j] -= (self.learningRate * delta_hidden[j]) # 更新隐藏层的偏置,使用梯度下降法# 定义一个函数,用于绘制每个迭代的误差值def show_err_graphic(self,v_error,v_epoch): # 定义一个函数,接受两个参数,分别是误差值和迭代次数的列表plt.figure(figsize=(9,4)) # 创建一个图像对象,设置大小为9x4plt.plot(v_epoch, v_error, "-",color="b", marker=11) # 绘制误差值随迭代次数的变化曲线,设置颜色和标记plt.xlabel("Number of Epochs") # 设置x轴的标签plt.ylabel("Squared error (MSE) ") # 设置y轴的标签plt.title("Error Minimization") # 设置标题plt.show() # 显示图像# 定义用于预测测试数据的predict函数def predict(self, X, y): # 定义一个函数,接受两个参数,分别是测试集的特征和标签my_predictions = [] # 定义一个空列表,用于存储预测值# 只进行前向传播forward = np.matmul(X,self.WEIGHT_hidden) + self.BIAS_hidden # 计算输入层到隐藏层的线性组合,加上隐藏层的偏置forward = np.matmul(forward, self.WEIGHT_output) + self.BIAS_output # 计算隐藏层到输出层的线性组合,加上输出层的偏置for i in forward: # 遍历输出层的每个节点my_predictions.append(max(enumerate(i), key=lambda x:x[1])[0]) # 将输出层的最大值对应的索引作为预测值# 打印预测值print(" Number of Sample | Class | Output | Hoped Output") # 打印表头for i in range(len(my_predictions)): # 遍历每个样本if(my_predictions[i] == 0): # 如果预测值为0,表示setosa类别print("id:{} | Iris-Setosa | Output: {} | Hoped Output:{} ".format(i, my_predictions[i], y[i])) # 打印样本的id,类别,输出值和期望值elif(my_predictions[i] == 1): # 如果预测值为1,表示versicolor类别print("id:{} | Iris-Versicolour | Output: {} | Hoped Output:{} ".format(i, my_predictions[i], y[i])) # 打印样本的id,类别,输出值和期望值elif(my_predictions[i] == 2): # 如果预测值为2,表示virginica类别print("id:{} | Iris-Iris-Virginica | Output: {} | Hoped Output:{} ".format(i, my_predictions[i], y[i])) # 打印样本的id,类别,输出值和期望值return my_predictions # 返回预测值列表pass# 定义用于训练过程的fit函数,使用训练数据def fit(self, X, y): # 定义一个函数,接受两个参数,分别是训练集的特征和标签count_epoch = 1 # 定义一个变量,用于记录迭代次数total_error = 0 # 定义一个变量,用于记录总误差n = len(X); # 定义一个变量,用于记录样本数epoch_array = [] # 定义一个空列表,用于存储迭代次数error_array = [] # 定义一个空列表,用于存储误差值W0 = [] # 定义一个空列表,用于存储隐藏层的权重W1 = [] # 定义一个空列表,用于存储输出层的权重while(count_epoch <= self.max_epochs): # 当迭代次数小于等于最大迭代次数时,循环执行for idx,inputs in enumerate(X): # 遍历训练集的每个样本,获取索引和输入self.output = np.zeros(self.classes_number) # 初始化输出为零向量# 阶段1 - (前向传播)self.OUTPUT_L1 = self.activation((np.dot(inputs, self.WEIGHT_hidden) + self.BIAS_hidden.T)) # 计算输入层到隐藏层的线性组合,加上隐藏层的偏置,然后通过激活函数,得到隐藏层的输出self.OUTPUT_L2 = self.activation((np.dot(self.OUTPUT_L1, self.WEIGHT_output) + self.BIAS_output.T)) # 计算隐藏层到输出层的线性组合,加上输出层的偏置,然后通过激活函数,得到输出层的输出# 阶段2 - One-Hot-Encodingif(y[idx] == 0): # 如果标签为0,表示setosa类别self.output = np.array([1,0,0]) # 输出为[1,0,0],表示第一个类别的概率为1,其他为0elif(y[idx] == 1): # 如果标签为1,表示versicolor类别self.output = np.array([0,1,0]) # 输出为[0,1,0],表示第二个类别的概率为1,其他为0elif(y[idx] == 2): # 如果标签为2,表示virginica类别self.output = np.array([0,0,1]) # 输出为[0,0,1],表示第三个类别的概率为1,其他为0square_error = 0 # 定义一个变量,用于记录平方误差for i in range(self.OutputLayer): # 遍历输出层的每个节点erro = (self.output[i] - self.OUTPUT_L2[i])**2 # 计算期望输出和实际输出的差的平方square_error = (square_error + (0.05 * erro)) # 将平方误差乘以0.05,累加到总的平方误差中total_error = total_error + square_error # 将平方误差累加到总误差中# 阶段3 - (反向传播):更新权重self.Backpropagation_Algorithm(inputs) # 调用反向传播算法的函数,传入输入作为参数total_error = (total_error / n) # 计算平均误差# 每个epoch打印一次误差值if((count_epoch % 50 == 0)or(count_epoch == 1)): # 如果迭代次数是50的倍数或者1,打印当前的迭代次数和误差值print("Epoch ", count_epoch, "- Total Error: ",total_error) # 打印迭代次数和误差值error_array.append(total_error) # 将误差值添加到误差值列表中epoch_array.append(count_epoch) # 将迭代次数添加到迭代次数列表中W0.append(self.WEIGHT_hidden) # 将隐藏层的权重添加到隐藏层权重列表中W1.append(self.WEIGHT_output) # 将输出层的权重添加到输出层权重列表中count_epoch += 1 # 迭代次数加一self.show_err_graphic(error_array,epoch_array) # 调用绘制误差值图像的函数,传入误差值列表和迭代次数列表# 打印训练期间获取的隐藏层权重print('') # 打印一个空行print('weight value of Hidden layer acquire during training: ') # 打印提示信息print(W0[0]) # 打印隐藏层权重列表的第一个元素,即初始的隐藏层权重# 打印训练期间获取的输出层权重print('') # 打印一个空行print('weight value of Output layer acquire during training: ') # 打印提示信息print(W1[0]) # 打印输出层权重列表的第一个元素,即初始的输出层权重return self # 返回自身对象
使用训练数据训练MLP模型

# 让我们尝试一下我们的MLPdictionary = {'InputLayer':4, 'HiddenLayer':5, 'OutputLayer':3,'Epochs':700, 'LearningRate':0.005,'BiasHiddenValue':-1,'BiasOutputValue':-1, 'ActivationFunction':'sigmoid'}# 定义一个字典,包含MLP模型的参数,如输入层、隐藏层、输出层的神经元个数,训练轮数,学习率,偏置值,激活函数Perceptron = MultiLayerPerceptron(dictionary)# 创建一个MultiLayerPerceptron类的实例,传入字典作为参数Perceptron.fit(train_X,train_y)# 调用fit方法,使用训练数据集train_X和train_y训练MLP模型
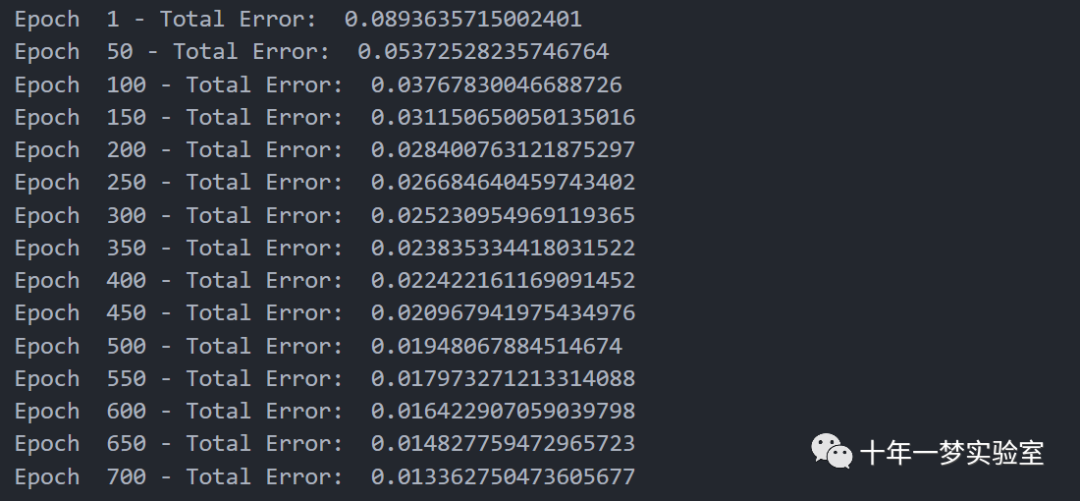
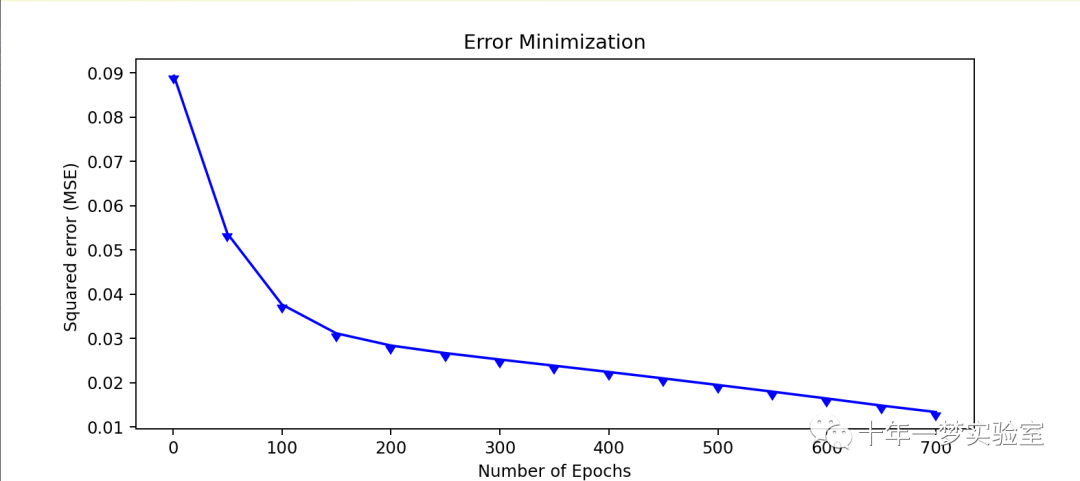
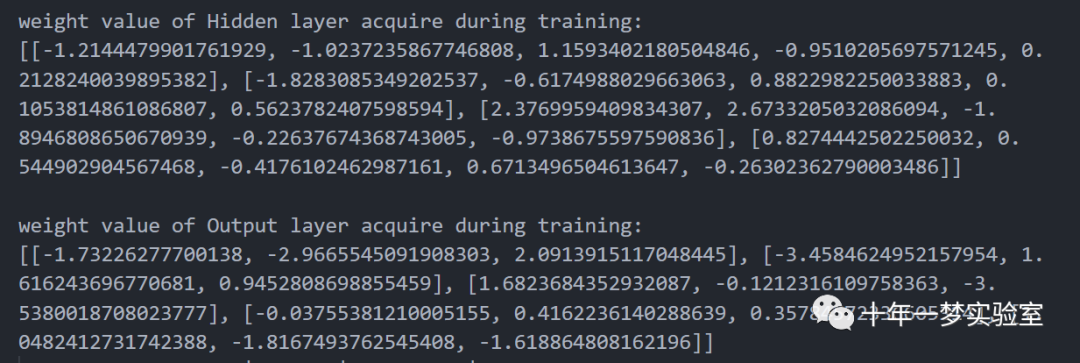
使用 MLP 模型预测测试数据
# 使用MLP模型预测测试数据pred = Perceptron.predict(test_X,test_y)# 调用predict方法,使用测试数据集test_X和test_y预测MLP模型的输出,返回一个列表pred,存储预测的类别pred = np.array(pred)# 将pred列表转换为numpy数组,方便后续计算true = test_y.astype('int')# 将test_y数组转换为整数类型,方便后续计算def compute_confusion_matrix(true, pred):'''用numpy计算两个np.arrays的混淆矩阵结果与以下相同(计算时间相似):"from sklearn.metrics import confusion_matrix"但是,此函数避免了对sklearn的依赖。'''# 定义一个函数,计算真实值和预测值的混淆矩阵,不需要使用sklearn库K = len(np.unique(true)) # Number of classes# 计算类别的个数,赋值给Kresult = np.zeros((K, K))# 创建一个K*K的零矩阵,用于存储混淆矩阵的结果for i in range(len(true)):# 遍历真实值的每个元素result[true[i]][pred[i]] += 1# 根据真实值和预测值的对应关系,将结果矩阵的相应位置加一return result# 返回结果矩阵conf_matrix = compute_confusion_matrix(true, pred)# 调用compute_confusion_matrix函数,传入真实值和预测值,得到混淆矩阵,赋值给conf_matrixprint('Confussion matrix result: ')# 打印混淆矩阵的结果print(conf_matrix)# 打印conf_matrix
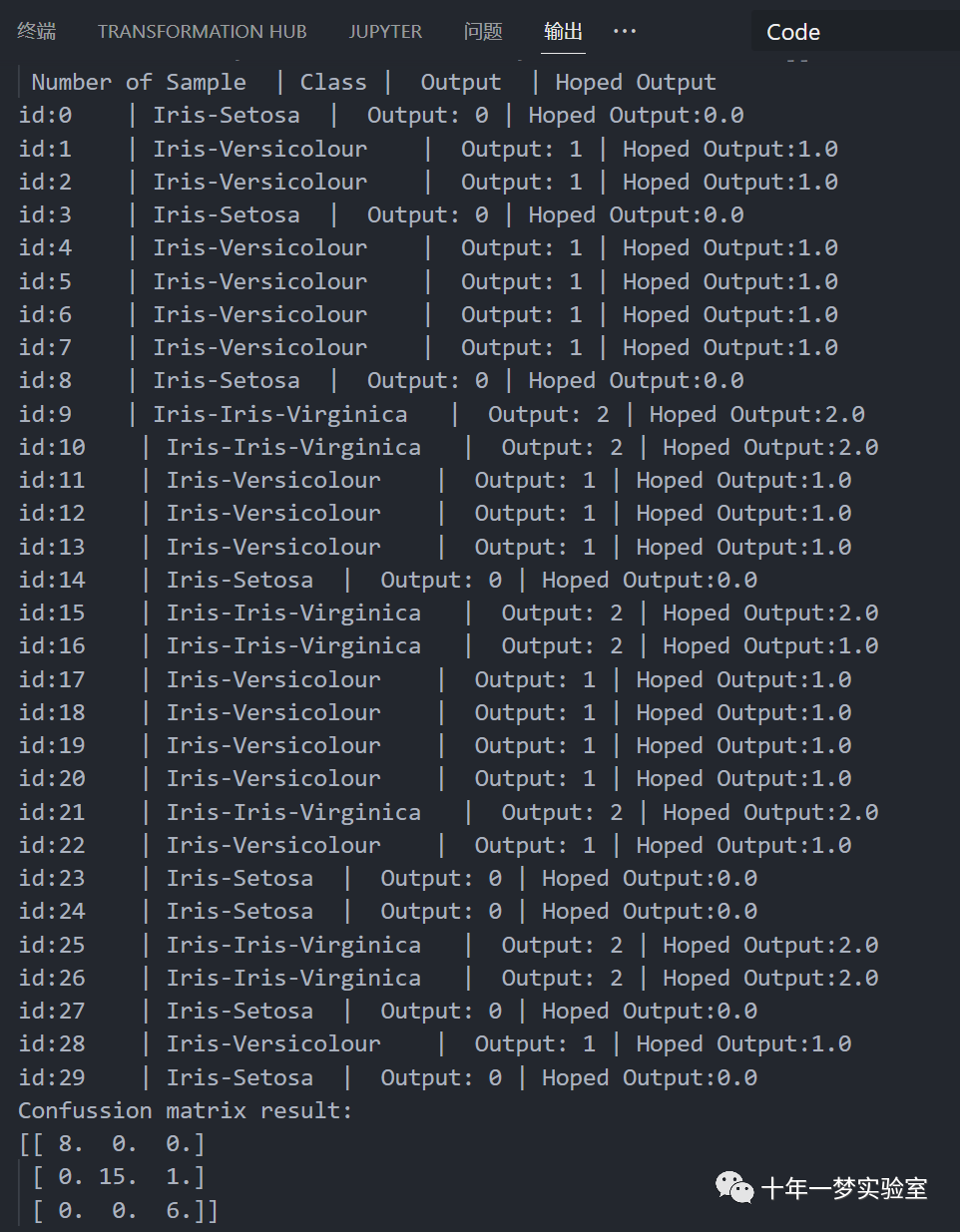
分类报告

# 分类报告classes = ['setosa ', 'versicolor', 'virginica ']# 定义一个列表,存储三个类别的名称def accuracy_average(confusion_matrix):# 定义一个函数,计算混淆矩阵的平均准确率diagonal_sum = confusion_matrix.trace()# 计算混淆矩阵的对角线之和,即正确分类的个数sum_of_all_elements = confusion_matrix.sum()# 计算混淆矩阵的所有元素之和,即总的样本个数return diagonal_sum / sum_of_all_elements# 返回对角线之和除以所有元素之和,即平均准确率def precision(label, confusion_matrix):# 定义一个函数,计算混淆矩阵的某个类别的精确度col = confusion_matrix[:, label]# 取混淆矩阵的第label列,即预测为该类别的个数return confusion_matrix[label, label] / col.sum()# 返回混淆矩阵的第label行第label列的元素,即正确预测为该类别的个数,除以第label列的元素之和,即精确度def recall(label, confusion_matrix):# 定义一个函数,计算混淆矩阵的某个类别的召回率row = confusion_matrix[label, :]# 取混淆矩阵的第label行,即真实为该类别的个数return confusion_matrix[label, label] / row.sum()# 返回混淆矩阵的第label行第label列的元素,即正确预测为该类别的个数,除以第label行的元素之和,即召回率def f1_score(label, confusion_matrix):# 定义一个函数,计算混淆矩阵的某个类别的F1分数num = precision(label, confusion_matrix) * recall(label, confusion_matrix)# 计算精确度和召回率的乘积,赋值给numdenum = precision(label, confusion_matrix) + recall(label, confusion_matrix)# 计算精确度和召回率的和,赋值给denumreturn 2 * (num/denum)# 返回2乘以num除以denum,即F1分数def precision_macro_average(confusion_matrix):# 定义一个函数,计算混淆矩阵的平均精确度rows, columns = confusion_matrix.shape# 获取混淆矩阵的行数和列数,赋值给rows和columnssum_of_precisions = 0# 初始化一个变量,用于存储所有类别的精确度之和for label in range(rows):# 遍历每个类别sum_of_precisions += precision(label, confusion_matrix)# 调用precision函数,计算该类别的精确度,累加到sum_of_precisionsreturn sum_of_precisions / rows# 返回sum_of_precisions除以rows,即平均精确度def recall_macro_average(confusion_matrix):# 定义一个函数,计算混淆矩阵的平均召回率rows, columns = confusion_matrix.shape# 获取混淆矩阵的行数和列数,赋值给rows和columnssum_of_recalls = 0# 初始化一个变量,用于存储所有类别的召回率之和for label in range(columns):# 遍历每个类别sum_of_recalls += recall(label, confusion_matrix)# 调用recall函数,计算该类别的召回率,累加到sum_of_recallsreturn sum_of_recalls / columns# 返回sum_of_recalls除以columns,即平均召回率def f1_score_average(confusion_matrix):# 定义一个函数,计算混淆矩阵的平均F1分数num = precision_macro_average(confusion_matrix) * recall_macro_average(confusion_matrix)# 计算平均精确度和平均召回率的乘积,赋值给numdenum = precision_macro_average(confusion_matrix) + recall_macro_average(confusion_matrix)# 计算平均精确度和平均召回率的和,赋值给denumreturn 2 * (num/denum)# 返回2乘以num除以denum,即平均F1分数print("label precision recall f1_score")# 打印标签,精确度,召回率,F1分数的表头for index in range(len(classes)):# 遍历每个类别print(f"{classes[index]} {precision(index, conf_matrix):9.3f} {recall(index, conf_matrix):6.3f} {f1_score(index, conf_matrix):6.3f}")# 打印该类别的名称,精确度,召回率,F1分数的表头print()print('Average accuracy: ', accuracy_average(conf_matrix))print('Average precision: ', precision_macro_average(conf_matrix))print('Average recall: ', recall_macro_average(conf_matrix))print('Average F1 score: ', f1_score_average(conf_matrix))
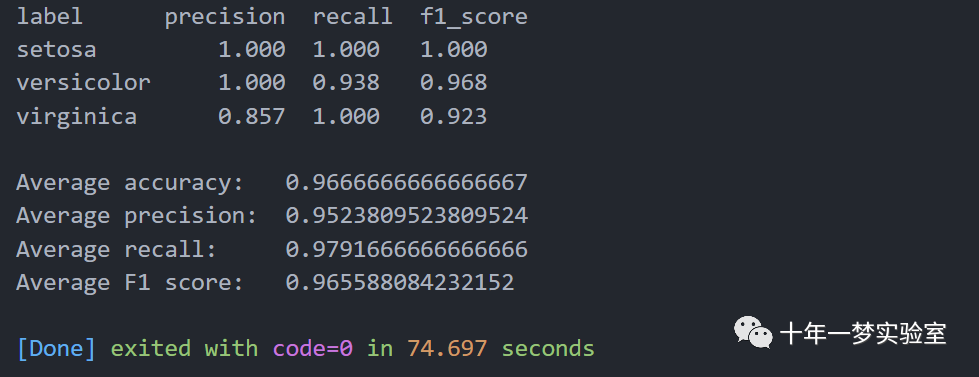
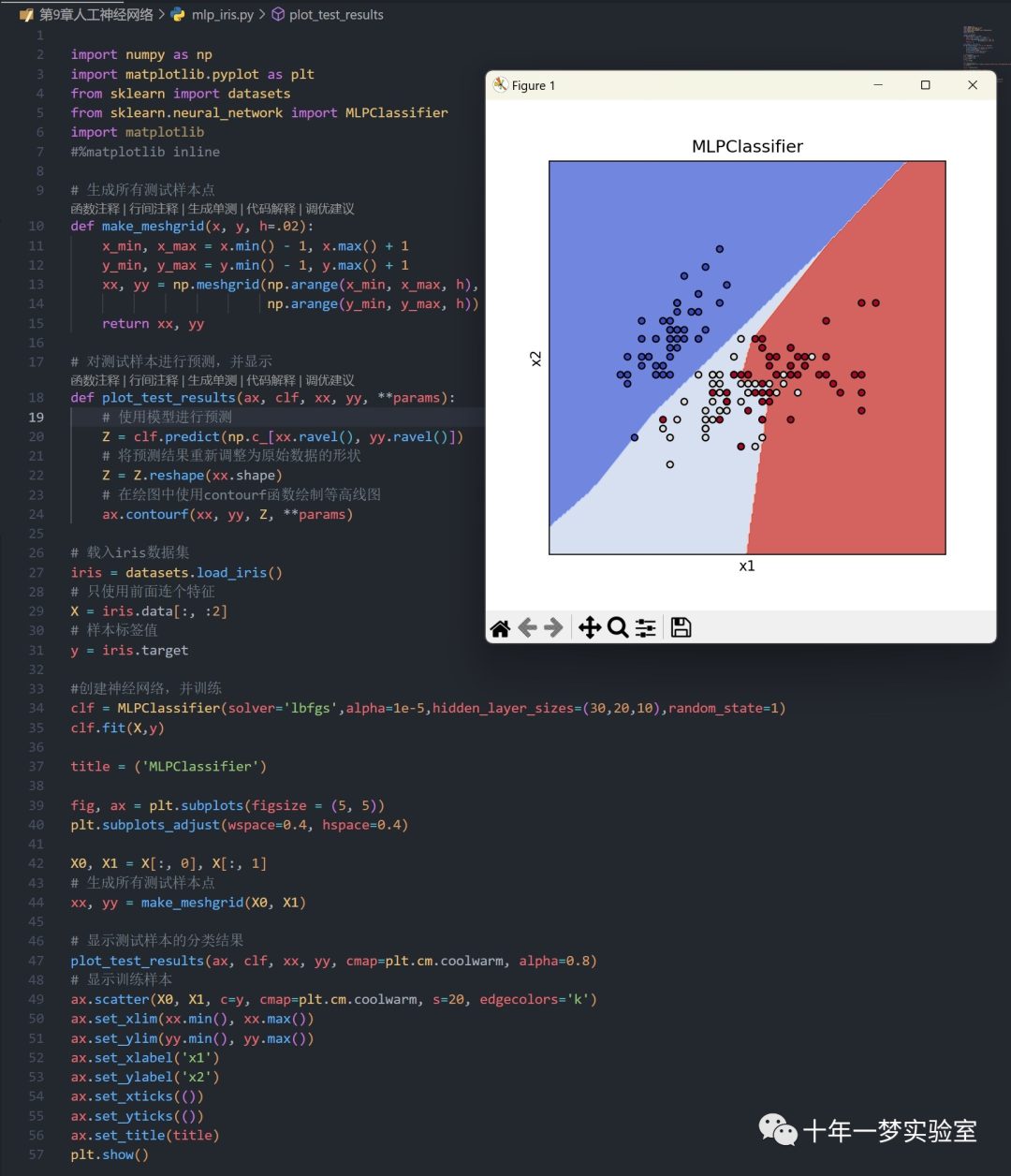
2.2 使用sklearn的MLP对iris数据集进行分类
三、一些问题




四、实现细节







五、人工神经网络的应用
人工神经网络解决分类和回归问题


人工神经网络应用场景

人工神经网络在制造业的应用
The End