人工智能算法之卷积神经网络(CNN)

卷积神经网络的训练过程分为两个阶段。

第一个阶段是数据由低层次向高层次传播的阶段，即前向传播阶段。

另一个阶段是，当前向传播得出的结果与预期不相符时，将误差从高层次向低层次进行传播训练的阶段，即反向传播阶段。

卷积神经网络网络通常包括以下几种层：

卷积层：卷积神经网络中每层卷积层由若干个卷积单元组成，每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征（如边缘、线条等），更多层的网络能从低级特征中迭代提取更复杂的特征。

修正线性单元层：这一层神经的活性化函数使用线性整流。

池化层：通常在卷积层之后会得到维度很大的特征，将特征切成几个区域，取其最大值或平均值，得到新的、维度较小的特征。

全连接层：把所有局部特征结合变成全局特征，用来计算最后每一类的得分。

图一 CNN示意图

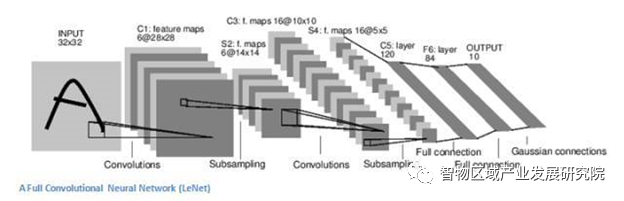
资料来源：知乎

（1）卷积层

图二  卷积层原理

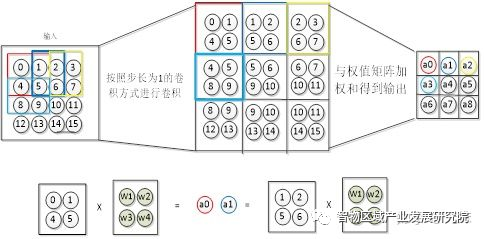
资料来源：知乎

卷积层的向前传播过程是通过卷积核对输入数据进行卷积操作得到卷积操作。数据在实际的网络中的计算过程以上图为例。其中一个输入为15个神经元的图片，卷积核为2×2×1的网络，即卷积核的权值为W1，W2，W3，W4。卷积核采用步长为1的卷积方式，卷积整个输入图片，形成了局部感受野，然后与其进行卷积算法，即权值矩阵与图片的特征值进行加权和（再加上一个偏置量）得到输出。

图三 层级连接方式

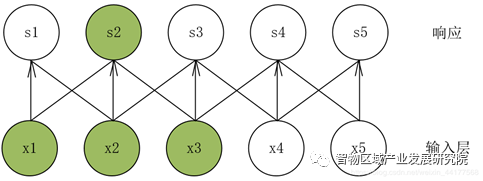
资料来源：CSDN

卷积运算的两个特性：

参数共享：在全联接的神经网络模型中，计算每层的输出时，权重矩阵中的元素只作用于某一个输入元素一次。而在卷积神经网络中，卷积核中的每一个元素将作用于每一个局部输入的特定位置上。根据参数共享的思想，我们只需要学习一组参数集合，而不需要针对每一个位置上的每一个参数来进行优化学习。

平移不变性：如果一个函数的输入做了一些改变，那么输出也跟着做出同样的改变，这就是平移不变性。平移不变性是由参数共享的物理意义所得。在计算机视觉中，假如要识别一个图片中是否有一只猫，那么无论这只猫在图片的什么位置，我们都应该识别出来，即就是神经网络的输出对于平移不变性来说是等变的。

（2）修正线性单元层（ReLU）

在每个卷积层之后，通常会立即应用一个非线性层（或激活层）。其目的是给一个在卷积层中刚经过线性计算操作（只是数组元素依次（element wise）相乘与求和）的系统引入非线性特征。过去，人们用的是像双曲正切和S型函数这样的非线性方程，但研究者发现ReLU层效果好得多，因为神经网络能够在准确度不发生明显改变的情况下把训练速度提高很多（由于计算效率增加）。它能帮助减轻梯度消失的问题——由于梯度以指数方式在层中消失，导致网络较底层的训练速度非常慢。ReLU层对输入内容的所有值都应用了函数 f(x) = max(0, x)。用基本术语来说，这一层把所有的负激活（negative activation）都变为零。这一层会增加模型乃至整个神经网络的非线性特征，而且不会影响卷积层的感受野。

（3）池化层

图像中的相邻像素倾向于具有相似的值，因此通常卷积层相邻的输出像素也具有相似的值，卷积层输出中包含的大部分信息都是冗余的。如果我们使用边缘检测滤波器并在某个位置找到强边缘，那么我们也可能会在距离这个像素1个偏移的位置找到相对较强的边缘。但是它们都一样是边缘，我们并没有找到任何新东西。池化层解决了这个问题。这个网络层所做的就是通过减小输入的大小降低输出值的数量。

图四 池化层示意图

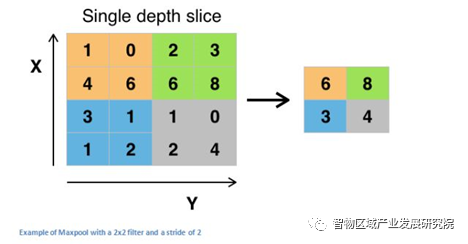
资料来源：知乎

常用的池化有均值池化和最大池化。

（4）全连接层

完全连接层观察上一层的输出（其表示了更高级特征的激活映射）并确定这些特征与哪一分类最为吻合。例如，如果该程序预测某一图像的内容为狗，那么激活映射中的高数值便会代表一些爪子或四条腿之类的高级特征。同样地，如果程序测定某一图片的内容为鸟，激活映射中的高数值便会代表诸如翅膀或鸟喙之类的高级特征。大体上来说，完全连接层观察高级特征和哪一分类最为吻合和拥有怎样的特定权重，因此当计算出权重与先前层之间的点积后，我们将得到不同分类的正确概率。

当卷积神经网络输出的结果与我们的期望值不相符时，则进行反向传播过程。求出结果与期望值的误差，再将误差一层一层的返回，计算出每一层的误差，然后进行权值更新。该过程的主要目的是通过训练样本和期望值来调整网络权值。误差的传递过程可以这样来理解，首先，数据从输入层到输出层，期间经过了卷积层，下采样层，全连接层，而数据在各层之间传递的过程中难免会造成数据的损失，则也就导致了误差的产生。而每一层造成的误差值是不一样的，所以当我们求出网络的总误差之后，需要将误差传入网络中，求得各层对于总的误差应该承担多少比重。

（1）全连接层之间的误差传递

求出网络的总差之后，进行反向传播过程，将误差传入输出层的上一层全连接层，求出在该层中，产生了多少误差。而网络的误差又是由组成该网络的神经元所造成的，所以我们要求出每个神经元在网络中的误差。求上一层的误差，需要找出上一层中哪些节点与该输出层连接，然后用误差乘以节点的权值，求得每个节点的误差。

（2）当前层为池化层，求上一层的误差

在池化层中，根据采用的池化方法，把误差传入到上一层。池化层如果采用的是最大池化（max-pooling）的方法，则直接把误差传到上一层连接的节点中。如果采用的是均值池化（mean pooling）的方法，误差则是均匀的分布到上一层的网络中。另外在池化层中，是不需要进行权值更新的，只需要正确的传递所有的误差到上一层。

（3）当前层为卷积层，求上一层的误差

卷积层中采用的是局部连接的方式，和全连接层的误差传递方式不同，在卷积层中，误差的传递也是依靠卷积核进行传递的。在误差传递的过程，我们需要通过卷积核找到卷积层和上一层的连接节点。求卷积层的上一层的误差的过程为：先对卷积层误差进行一层全零填充，然后将卷积层进行一百八十度旋转，再用旋转后的卷积核卷积填充过程的误差矩阵，并得到了上一层的误差。下图右上方为卷积层的向前卷积过程，而右下方为卷积层的误差传递过程。从图中可以看出，误差的卷积过程正好是沿着向前传播的过程，将误差传到了上一层。

图五 卷积层的误差传递过程

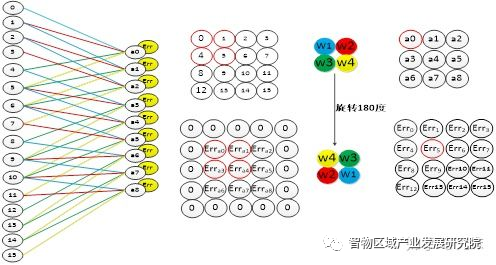
资料来源：知乎

卷积层的误差更新过程为：将误差矩阵当做卷积核，卷积输入的特征图，并得到了权值的偏差矩阵，然后与原先的卷积核的权值相加，并得到了更新后的卷积核。

（1）特征

全连接DNN的结构里下层神经元和所有上层神经元都能形成连接，带来的问题是参数数量的爆炸。假设输入的是一幅像素为1K*1K的图像，隐含层有1M个节点，这一层就有10的12次方个权重需要训练。这不仅容易过拟合，而且极容易陷入局部最优。由于数据中固有的局部模式（比如图像的轮廓等）可以利用，显然应该将其和神经网络技术相结合，这就是CNN模型。通过CNN模型，能够瞬间实现参数数量的下降，这使得我们能够用已有的数据得到良好的模型，这便是CNN的特征。

（2）适用性

虽然我们一般把CNN和图片联系在一起，但是事实上根据CNN的特性，其可以处理大部分在跨区域上有关联的格状结构化数据。比如，顺着同样的思路，利用语音语谱结构中的局部信息，CNN照样能应用在语音识别中。